Overview

This document provides an overview of how Seldonian algorithms (SAs) are implemented using this library. For a detailed description of what SAs are, see the Seldonian Machine Learning Toolkit homepage. In addition to this overview page, we have created a few hands-on tutorials illustrating how to use this library on simulated datasets and more realistic datasets: Toolkit tutorials.

The most important piece of the Seldonian Engine API is the SeldonianAlgorithm class. One can run a Seldonian algorithm with a single API call using this class:

from seldonian.seldonian_algorithm import SeldonianAlgorithm
from seldonian.utils.io_utils import load_pickle
# here, the spec object is loaded from a file
spec = load_pickle('spec.pkl')
SA = SeldonianAlgorithm(spec)
SA.run()

In this overview, we will go over what is in the spec object and how to create it. We will also cover what SA.run() actually does.

Note: The Engine supports supervised learning and reinforcement learning (RL) Seldonian algorithms. Where we could, we unified the code to work for both regimes. The general pattern in the API is a regime-independent base class from which two child classes inherit, one for each of the two regimes.

Interface

The interface is a general concept for how the user provides inputs to the SA. For a full conceptual description, see the Seldonian Toolkit Overview. In the interface, the user provides (at minimum):

• the data

• the metadata

• the Behavioral constraints they want the SA to enforce.

The interface outputs a Spec object, which consists of a complete specification used to run the seldonian algorithm.

Note: The Engine library is not an interface. In general, it is up to a developer to design the interface for their specific application. We provide some example interfaces as part of the Seldonian Toolkit: a command line interface and a graphical user interface.

Spec object

The “spec” object (short for specification object) contains all of the inputs needed to run the Seldonian algorithm, the most important of which are:

• the dataset

• the underlying machine learning model

• the behavioral constraints

Each of these is represented by an object in the Engine API, as we will discuss below.

The seldonian.spec module contains the classes used to define spec objects. For the supervised learning regime, the SupervisedSpec class is used, and for the reinforcement learning regime the RLSpec class is used. We provide convenience functions to create these objects: createSupervisedSpec() for supervised learning and createRLspec() for reinforcement learning.

Dataset object

The dataset module contains the SupervisedDataSet (supervised learning) and the RLDataSet (reinforcement learning) classes. These objects contain the data points (supervised learning) or episodes (reinforcement learning) as well as metadata. They can be constructed manually, but we also provide a DataSetLoader class containing several convenience methods for loading data from files or arrays into the dataset objects.

For supervised learning, one can create a SupervisedDataSet object from a data file and metadata file using the load_supervised_dataset() method, for example:

from seldonian.dataset import DataSetLoader
loader = DataSetLoader(regime='supervised_learning')
dataset = loader.load_supervised_dataset(
        filename,
        metadata_filename)

The filename parameter must point to a data file consisting of rows of numbers (or arrays) that are comma-separated and have no header. Categorical columns must be numerically encoded. For example, a supervised learning data file format might look like:

0,1,622.6,491.56,439.93,707.64,663.65,557.09,711.37,731.31,509.8,1.33333
1,0,538.0,490.58,406.59,529.05,532.28,447.23,527.58,379.14,488.64,2.98333
1,0,455.18,440.0,570.86,417.54,453.53,425.87,475.63,476.11,407.15,1.97333
0,1,756.91,679.62,531.28,583.63,534.42,521.4,592.41,783.76,588.26,2.53333
...

where each row represents a different data point and each column is a feature or a label. All sensitive attributes must be one-hot encoded. In this example, the first two columns are sensitive attributes, columns 3-11 are features, and the last column is the label column. The engine currently only supports a single label column for supervised learning.

For reinforcement learning, one can create a RLDataSet object from a data file and (optionally) a metadata file. There are two supported methods for loading data, depending on the format of the data file. For example:

from seldonian.dataset import DataSetLoader
loader = DataSetLoader(regime='reinforcement_learning')
# method 1
dataset = loader.load_RL_dataset_from_csv(
        filename)
# method 2
dataset = loader.load_RL_dataset_from_episode_file(
        filename)

In the first method, the comma-separated file (CSV) must have no header. Each row represents a single timestep and the columns must correspond to the episode index, observation, action, rewards, action probability. The observations can be arrays or single numbers. An example file with 10 episodes where observations and actions have integer types might look like this:

0,0,0,0,0.25
0,0,1,0,0.25
0,1,2,0,0.25
0,4,1,0,0.25
0,5,0,0,0.25
...
9,1,2,0,0.25
9,4,1,0,0.25
9,5,0,0,0.25
9,2,2,0,0.25
9,5,2,1,0.25
...

In the second method, the episode file must be a pickle file containing a list of Episode objects.

Regardless of the regime and file format, the data file should include all of the data you have, i.e., before partitioning into train, test, validation splits. The Engine will partition the data internally into candidate data and safety data in order to run the Seldonian algorithm. The column names are intentionally excluded from the data files and are provided in a separate metadata file, via the metadata_filename parameter. In the RL case, the meanings of the columns are fixed so column names are not necessary.

The metadata file must be a JSON-formatted file containing several required key:value pairs depending on the regime of your problem. For supervised learning, the required keys are:

• regime, set to supervised_learning in this case

• sub_regime, either classification or regression

• columns, a list of all of the column names in your data file

• label_column, the name of the column that you are trying to predict

• sensitive_columns, a list of the column names for the sensitive attributes in your dataset

For reinforcement learning, this file is optional, but if provided, the required keys are:

• regime, which is set to ‘reinforcement_learning’ in this case

• columns, (optional) a list of the column names in your data file

Model object

The biggest split between supervised and reinforcement learning in the Engine API is in how the underlying machine learning model is represented. Supervised learning models are represented as classes in the module: models.models. The base class for classification (regression) is: ClassificationModel (RegressionModel). Any supervised learning model must inherit from either of these classes or one of their child classes. Some useful classes have already been created for running the tutorials, such as LinearRegressionModel and LogisticRegressionModel. These classes essentially wrap scikit-learn’s model classes, for example, their LinearRegression model.

Unless you are writing your own model, you will likely only need to know which of these models best fits your application. You may also want to choose from the primary objective functions, which are written as methods of the class. The primary objective function is one of the inputs to the spec object, though a default will be chosen if you do not explicitly pass one to the spec object.

The reinforcement learning model is represented by the RL_model class. This object takes as input a policy parameterization and environment-specific information, two things which supervised learning models do not have. The base policy class, Policy must be inherited in a user-defined policy class. We have provided example policies, such as the Softmax policy and DiscreteSoftmax policy, to illustrate how to extend the base classes to create your own RL policies. The environment-specific information is provied via the env_kwargs dictionary parameter to the :py:class`.RL_model` object. This dictionary is used to pass parameters such as \({\gamma}\), the discount factor, that are used in calculating importance sampling estimates.

Behavioral constraints

In the definition of a Seldonian algorithm, behavioral constraints, \((g_i,{\delta}_i)_{i=1}^n\) are of a set of constraint functions, \(g_i\), and confidence levels, \({\delta}_i\). Constraint functions need not be provided to the interface directly, but are often built by the engine from constraint strings provided by the user.

Constraint strings

Constraint strings contain the mathematical definition of the constraint functions, \(g_i\). These strings are written as Python strings and support five different types of sub-strings.

1. The following math operators:

• +, -, *, /

2. These four native Python math functions:

• min()

• max()

• abs()

• exp()

3. Constants. These can be integers or floats, such as 4 or 0.239.

4. Custom strings that trigger a call to a custom function. There are a set of special strings we call “measure functions” that correspond to statistical functions. For example, if Mean_Squared_Error appears in a constraint string, the mean squared error will be calculated internally. Measure functions are specific to the machine learning regime. For a full list of currently supported measure functions, see: parse_tree.operators. We left open the possibility that developers will want to define their own measure functions by adding to the current list. Measure functions are defined to estimate the confidence bounds on the mean value of a quantity. It is possible developers will want to bound something other than the mean, or do it in a way that differs from how we implemented bounds in the Engine. They would do this by creating their own custom base nodes. We wrote the custom base node tutorial to instruct new users how to create their own measure functions as well as custom base nodes.

5. The inequality strings “<=” or “>=”. These are optional. Recall from the definition of a Seldonian algorithm that we want \(g_i{\leq}0\) to be satisfied. However, it can be cumbersome to write all of your constraint strings with a “<= 0” at the end. For convenience, we support constraint strings that both include and exclude the inequality symbols. For example, the four expressions will all be interpreted identically by the engine:

• “Mean_Squared_Error <= 4.0”

• “Mean_Squared_Error - 4.0 <= 0”

• “Mean_Squared_Error - 4.0”

• “4.0 >= Mean_Squared_Error”

Constraint strings with more than one inequality string or with “>”, “<”, or “=” by themselves are not supported and will result in an error when the Engine tries to parse the constraint string.

Here are a few examples of basic constraint strings and their plain English interpretation:

• Mean_Squared_Error - 2.0: “Ensure that the mean squared error is less than or equal to 2.0”. Here, Mean_Squared_Error is a special measure function for supervised regression problems.

• 0.88 <= TPR: “Ensure that the True Positive Rate (TPR) is greater than or equal to 0.88”. Here, TPR is a measure function for supervised classification problems.

• J_pi_new >= 0.5: “Ensure that the performance of the new policy (J_pi_new) is greater than or equal to 0.5”. Here, J_pi_new is a measure function for reinforcement learning problems.

These basic constraint strings cover a number of use cases. However, they do not use information about the sensitive attributes (columns) in the dataset, which commonly appear in fairness definitions. The Engine supports a specification for filtering the data used to calculate the bound on the quantity defined by the measure function over one or more sensitive attributes. This is only supported for supervised learning datasets. The specification for doing this is as follows:

(measure_function | [ATR1,ATR2,...])

where measure_function is a placeholder for the actual measure function in use and [ATR1,ATR2,...] is a placeholder list of attributes (column names) from the dataset. The parentheses surrounding the statement are required in all cases.

Let’s say that an example dataset has four sensitive attributes: [M,F,R1,R2], standing for “male”, “female”, “race class 1”, “race class 2”). The following constraint strings are examples of valid uses of measure functions subject to sensitive attributes.

• abs((PR | [M]) - (PR | [F])) <= 0.15: “Ensure that the absolute difference between the positive rate (the meaning of the measure function “PR”) for males (M) and the positive rate for females (F) is less than or equal to 0.15”. This constraint is called demographic parity (with a tolerance of 15%). Here, M and F must be columns of the dataset, and specified both in the columns key and the sensitive_columns key in the Metadata file. We also see the use of a native Python function, :code:`abs(), in this constraint string.

• 0.8 - min((PR | [M])/(PR | [F]),(PR | [F])/(PR | [M])): “Ensure that ratio of the positive rate for males (M) to the positive rate for females (F) or the inverse ratio is at least 0.8.” This constraint is called disparate impact (with a tolerance of 0.8). We see the use of min(), another native Python function in this constraint string.

It is permitted to use more than one attribute for a given measure function. For example:

• (FPR | [F,R1]) <= 0.2: “Ensure that the false positive rate (FPR) for females (F) belonging to race class 1 (R1) is less than or equal to 0.2.

Note that the constraint strings only make up part of the behavioral constraints. The user must also specify the values of \({\delta}\) for each provided constraint string. The Engine bundles the list of behavioral constraints into ParseTree objects. The list of parse trees is one of the required inputs to the Spec object.

What does SA.run() do?

The SeldonianAlgorithm object takes as input the spec object (required) and some optional parameters. Once this object is created, the Seldonian algorithm can be run via the SeldonianAlgorithm.run() method, as shown in the code block at the top of this page. At a broad scope, this method runs candidate selection, followed by the safety test and returns the tuple: passed_safety, solution, where passed_safety is a boolean indicating whether the safety test passed and solution is either the string "NSF" standing for “No Solution Found” or an array of model weights of the fitted model if a solution was found.

All of the details of how to run candidate selection and the safety test are passed throught the spec object. We will now go into more detail as to what actually happens in the Engine code during candidate selection and the safety test.

Candidate Selection

The goal of candidate selection is to find a solution to the Seldonian ML problem which is likely to pass the safety_test. Candidate selection always returns a solution, even if the probability of passing the safety test is small. Candidate selection has a method CandidateSelection.run() which runs an optimization process to find the solution. There are currently two supported optimization techniques for candidate selection, controlled by the optimization_technique parameter of the spec object. The two supported values of this parameter are:

1. barrier_function: Black box optimization with a barrier function. This is currently only supported for supervised learning problems. In this case, a barrier, which is shaped like the upper bound functions, is added to the cost function when any of the constraints are violated. This forces solutions toward the feasible set. When this optimization technique is used, the optimizer parameter of the spec object can take on of these five values: "Powell", "CG", "Nelder-Mead", "BFGS", "CMA-ES". The first four use Scipy’s minimize function, where the optimizer string, e.g., "Powell" refers to the solver method. If optimizer="CMA-ES" then a Covariance matrix adaptation evolution strategy) is used, which is implemented using the cma Python package. Optimization hyperparameters for these solvers can be passed via the optimization_hyperparams parameter to the spec object.

2. gradient_descent: Gradient descent on a Lagrangian. For details on the form of the Lagrangian and the KKT optimization strategy see the Algorithm details tutorial of the Seldonian Toolkit homepage.

In situations where the contraints are conflicting with the primary objective, vanilla gradient descent can result in oscillations of the solution near the feasible set boundary. These oscillations can be dampened using momentum in gradient descent. We implemented the adam optimizer as part of our gradient descent method, which includes momentum, and found that it mitigates the oscillations in all problems we have tested so far. optimizer="adam is the only acceptable value to the spec object if optimization_technique="gradient_descent".

One can visualize the values of \(\hat{f}\), \(\lambda_i\), \(\hat{g}_i\), and the Lagrangian, \(\mathcal{L(\theta,\lambda)}\) using a plotting utility function. These values are saved in a log file if the following flag is set when the Seldonian algorithm is ran, i.e.,

SA.run(write_cs_logfile=True)

The file is pickled and saved in a logs/ directory with the naming convention: candidate_selection_log{N}.p, where N starts at 0 and then increases such that the log files are not overwritten. These files can be visualized using the function seldonian.utils.plot_utils.plot_gradient_descent(), for example:

from seldonian.utils.io_utils import load_pickle
from seldonian.utils.plot_utils import plot_gradient_descent
log_file = "candidate_selection_log0.p"
cs_dict = load_pickle(log_file)
plot_gradient_descent(cs_dict,primary_objective_name="log loss",show=True)

Here is an example of the plot produced using this function:

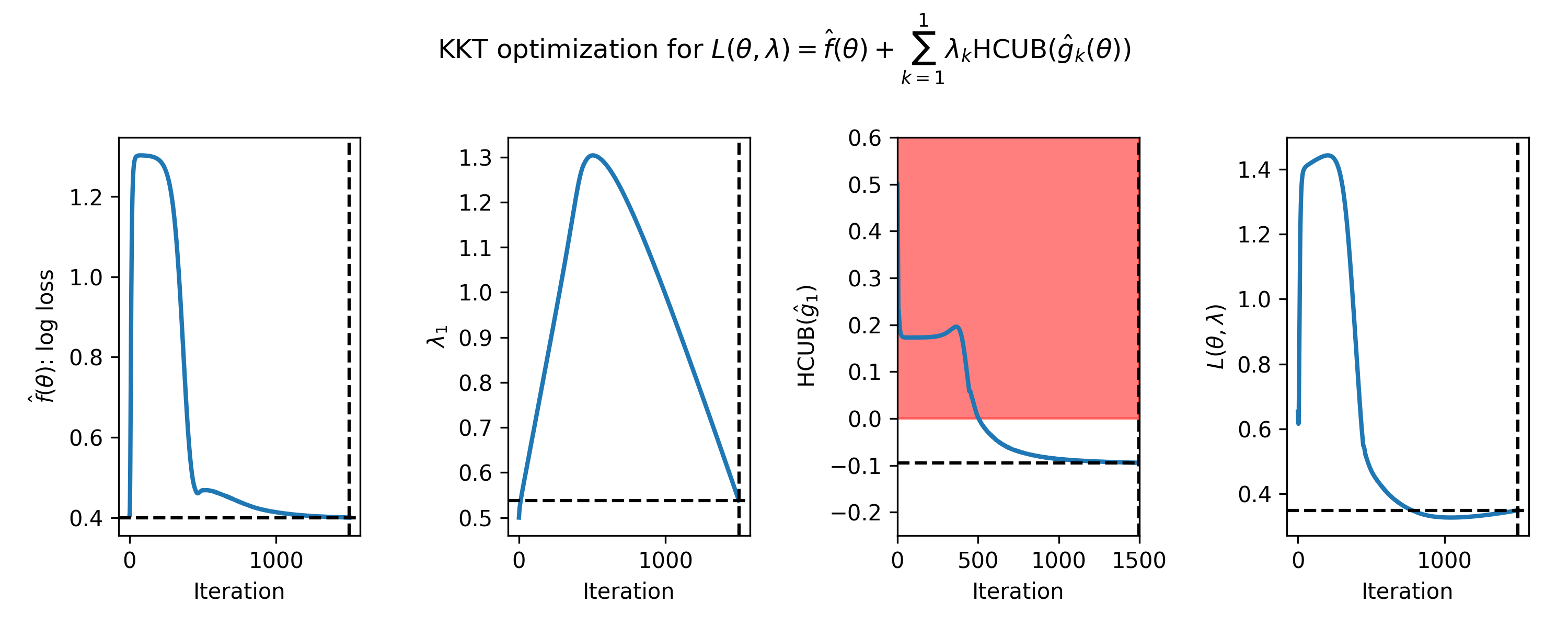
Figure 1: The evolution of parameters during 1500 iterations of gradient descent for a Seldonian algorithm with a single behavioral constraint. The red area in the right middle plot indicates the region where the constraint is predicted to be violated in the safety test. The dotted black lines indicate where the optimal solution was found.

In the case of multiple constraints, each constraint gets its own row. The primary objective (left) and Lagrangian (right) subplots are repeated in each row in that case.

Safety Test

The safety test is run on the solution found during candidate selection. The safety test has a method SafetyTest.run() which runs the safety test and returns a boolean flag passed deeming whether the solution found during candidate selection passed the safety test. Like candidate selection, the inputs to the safety test are assembled from the spec object. You should not need to interact with the safety test API directly.