Implementing a convolutional neural network with PyTorch
In this section, we will build a CNN in PyTorch that is compatible with the Seldonian Toolkit. First, make sure you have the latest version of the engine installed.
$ pip install --upgrade seldonian-engine
Next, install the PyTorch and torchvision Python packages. These packages are not installed as part of the Seldonian Engine. Usually, one can just do:
$ pip install torch
$ pip install torchvision
Note: To enable GPU acceleration, you will need to have the proper setup for your machine. For example, CUDA needs to be enabled if you have an NVIDIA graphics card. This may require more than simply doing pip install torch. The good news is that even if you don't have access to a GPU, you will still be able to run the model on your CPU. To learn more about GPU-acceleration for PyTorch, see the "Install Pytorch" section of this page: https://pytorch.org/
It is important to make a clear distinction when referring to "models" throughout this tutorial. We will use the term "Seldonian model" to refer to the highest level model abstraction in the toolkit. The Seldonian model is the thing that communicates with the rest of the toolkit. The Seldonian model we will build in this tutorial consists of a "PyTorch model," a term which we will use to refer to the actual PyTorch implementation of the neural network. The PyTorch model does not communicate with the other pieces of the Seldonian Toolkit, whereas the Seldonian model does.
Seldonian models are implemented as Python classes. There are three requirements for creating a new Seldonian model class with PyTorch:
- The class must inherit from this base class:
seldonian.models.pytorch_model.SupervisedPytorchBaseModel.
- The class must take as input a
device string, which specifies the hardware (e.g. CPU vs. GPU) on which to run the model, and pass that device string to the base class's __init__ method.
- The class must have a
create_model() method in which it defines the PyTorch model and returns it as an instance of torch.nn.Module or torch.nn.Sequential. The reason for this is that the PyTorch model must have a forward() method, and these are two common model classes that have that method.
We will name our new model
PyTorchCNN and use the network architecture described in this article:
https://medium.com/@nutanbhogendrasharma/pytorch-convolutional-neural-network-with-mnist-dataset-4e8a4265e118. This is an overview of the flow of the network:
Sequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(4): ReLU()
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Flatten(start_dim=1, end_dim=-1)
(7): Linear(in_features=1568, out_features=10, bias=True)
(8): Softmax(dim=1)
)
This model has around 29,000 parameters. We consider the Conv2d, ReLU, and MaxPool2d to be a single hidden layer, such that this network comprises two hidden layers, followed by a single output Linear+Softmax layer.
Here is the implementation of the Seldonian model that implements this PyTorch model, meeting the three requirements specified above.
from seldonian.models.pytorch_model import SupervisedPytorchBaseModel
import torch.nn as nn
class PytorchCNN(SupervisedPytorchBaseModel):
def __init__(self,device):
""" Implements a CNN with PyTorch.
CNN consists of two hidden layers followed
by a linear + softmax output layer
:param input_dim: Number of features
:param output_dim: Size of output layer (number of label columns)
"""
super().__init__(device)
def create_model(self,**kwargs):
""" Create the pytorch model and return it
Inputs are N,1,28,28 where N is the number of them,
1 channel and 28x28 pixels.
Do Conv2d,ReLU,maxpool twice then
output in a fully connected layer to 10 output classes
and softmax outputs to get probabilities.
"""
cnn = nn.Sequential(
nn.Conv2d(
in_channels=1,
out_channels=16,
kernel_size=5,
stride=1,
padding=2,
),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2),
nn.Conv2d(16, 32, 5, 1, 2),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(32 * 7 * 7, 10),
nn.Softmax(dim=1)
)
return cnn
It is very important that the create_model() method returns the PyTorch model object. In this implementation, we used PyTorch's sequential container to hold a sequence of Pytorch nn.Modules. This is just one pattern that PyTorch provides, and it is not required in the create_model() method. As long as this method returns a PyTorch model object that has a forward() method, it should be compatible with the toolkit. Also note that we applied a softmax layer at the end of the model so that the outputs of the model are probabilities instead of logits. We did this because the primary objective function we will use when we run the model in the following example expects probabilities. This might not always be the case for your use case, so be aware of what your objective function expects from your model.
At this point, this model is ready to use in the toolkit.
MNIST with a safety constraint
The Modified National Institute of Standards and Technology (MNIST) database is a commonly used dataset in machine learning research. It contains 60,000 training images and 10,000 testing images of the handwritten digits 0-9. Yes, there are models that are superior to the simple CNN we built in terms of accuracy (equivalently, error rate), but objective in this tutorial is to show how to create a Seldonian version of a PyTorch deep learning model, not to achieve maximum accuracy.
We first need to define the standard machine learning problem in the absence of constraints. We have a multiclass classification problem with 10 output classes. We could train the two-hidden-layer convolutional neural network we defined in the previous section to minimize some cost function. Specifically, we could use gradient descent to minimize the cross entropy (also called logistic loss for multiclass classification problems).
Now let's suppose we want to add a safety constraint. One safety constraint we could enforce is that the accuracy (the fraction of correctly labeled digits across all 10 classes) of our trained model must be at least 0.95, and we want that constraint to hold with 95% confidence. The problem can now be fully formulated as a Seldonian machine learning problem:
Using gradient descent on the CNN we defined in the previous section, minimize the cross entropy of the model, subject to the safety constraint:
- $g_1$ : $\text{ACC} - 0.95$ (equivalent to $\text{ACC} <= 0.95$), and $\delta=0.05$, where $\text{ACC}$ is the measure function for accuracy.
Note that if this safety constraint is fulfilled, we can have high confidence ([$1-\delta$]-confidence) that the accuracy of the model, when applied to unseen data, is at least 0.95. This is
not a property of even the most sophisticated models that can achieve accuracies of $\gt0.999$ on MNIST.
Running the Seldonian algorithm
If you are reading this tutorial, chances are you have already used the engine to run Seldonian algorithms. If not, please review the Fair loans tutorial. We need to create a SupervisedSpec object, consisting of everything we will need to run the Seldonian algorithm. We will write a script that does this and then runs the algorithm. First, let's define the imports that we will need. The PytorchCNN model that we defined above is already part of the library, living in a module called seldonian.models.pytorch_cnn, so we can import the model from that module.
#pytorch_mnist.py
import autograd.numpy as np # Thinly-wrapped version of Numpy
from seldonian.spec import SupervisedSpec
from seldonian.dataset import SupervisedDataSet
from seldonian.models.pytorch_cnn import PytorchCNN
from seldonian.models import objectives
from seldonian.seldonian_algorithm import SeldonianAlgorithm
from seldonian.parse_tree.parse_tree import (
make_parse_trees_from_constraints)
import torch
from torchvision import datasets
from torchvision.transforms import ToTensor
Next, set a random seed so that we can reproduce the result each time we run the script, set the regime and subregime of the problem, and then fetch the data. We obtain the data using PyTorch's torchvision API, which provides a copy of the MNIST dataset. We will retrieve the training and test sets using download=True to download the data (64 MB) to a folder on your computer data_folder the first time you run the script. If you run the script again, it will not redownload the data, but will look in your data_folder for an existing copy of the data. We combine the train and test sets and then extract the features and labels from the combined data. The Seldonian algorithm will partition these into candidate and safety data according to the value of frac_data_in_safety that we specify in the spec object. In this example, we will use frac_data_in_safety=0.5.
if __name__ == "__main__":
torch.manual_seed(0)
regime='supervised_learning'
sub_regime='multiclass_classification'
data_folder = './data'
train_data = datasets.MNIST(
root = data_folder,
train = True,
transform = ToTensor(),
download = True,
)
test_data = datasets.MNIST(
root = data_folder,
train = False,
transform = ToTensor(),
download = True,
)
# Combine train and test data into a single tensor of 70,000 examples
all_data = torch.vstack((train_data.data,test_data.data))
all_targets = torch.hstack((train_data.targets,test_data.targets))
N=len(all_targets)
assert N == 70000
frac_data_in_safety = 0.5
features = np.array(all_data.reshape(N,1,28,28),dtype='float32')/255.0
labels = np.array(all_targets) # these are 1D so don't need to reshape them
Notice that we reshaped the features, changed their data type, divided all of the pixel values by 255.0. This is all done so that the features are compliant with the input layer of the model. We also converted them to NumPy arrays, a necessary step even though they will get converted back to Tensors before they are fed into the model. The reason why we have to do this is beyond the scope of this tutorial and will be explained in a future tutorial. Next, let's create the SupervisedDataset object.
meta_information = {}
meta_information['feature_col_names'] = ['img']
meta_information['label_col_names'] = ['label']
meta_information['sensitive_col_names'] = []
meta_information['sub_regime'] = sub_regime
dataset = SupervisedDataSet(
features=features,
labels=labels,
sensitive_attrs=[],
num_datapoints=N,
meta_information=meta_information)
There are no sensitive attributes in this dataset. Recall that the constraint we defined is that the accuracy should be at least $0.95$ with a confidence level of $\delta=0.05$. We create this constraint as follows:
constraint_strs = ['ACC >= 0.95']
deltas = [0.05]
parse_trees = make_parse_trees_from_constraints(
constraint_strs,deltas,regime=regime,
sub_regime=sub_regime)
Now, let's create the model instance, specifying the device we want to run the model on.
device = torch.device("mps")
model = PytorchCNN(device)
In my case, I am running the script on an M1 Macbook Air that has a GPU. To specify that I want to do the model computations using this GPU, I use the device string "mps". If you have an NVIDIA chip (common on modern Windows machines), you can try the device string "cuda". The worst that will happen is you'll get an error message of the sort:
AssertionError: Torch not compiled with CUDA enabled
If you do not have a GPU enabled, you can run on the CPU by using the device string "cpu". If you are not sure, you can check if cuda is available by doing:
import torch
print(torch.cuda.is_available())
If this prints True, then you should be able to use cuda as your device string. Similarly, on a mac with an M1 chip, you can check if the Metal Performance Shaders (MPS) driver is available by doing:
import torch
print(torch.backends.mps.is_available())
print(torch.backends.mps.is_built())
If both are True, then you should be able to use "mps" as your device. If not, see this page for help setting up your environment to use the MPS driver: https://towardsdatascience.com/installing-pytorch-on-apple-m1-chip-with-gpu-acceleration-3351dc44d67c
Now that the model is instantiated, we can get the randomized initial weights that PyTorch assigned to the parameters and use that as the initial values of $\theta$, the model weights, in gradient descent. We can also now specify that we want to use the cross entropy for our primary objective function, which is called multiclass_logistic_loss in the toolkit:
initial_solution_fn = model.get_initial_weights
primary_objective_fn = objectives.multiclass_logistic_loss
We are now ready to create the spec object:
spec = SupervisedSpec(
dataset=dataset,
model=model,
parse_trees=parse_trees,
frac_data_in_safety=frac_data_in_safety,
primary_objective=primary_objective_fn,
use_builtin_primary_gradient_fn=False,
sub_regime=sub_regime,
initial_solution_fn=initial_solution_fn,
optimization_technique='gradient_descent',
optimizer='adam',
optimization_hyperparams={
'lambda_init' : np.array([0.5]),
'alpha_theta' : 0.001,
'alpha_lamb' : 0.01,
'beta_velocity' : 0.9,
'beta_rmsprop' : 0.95,
'use_batches' : True,
'batch_size' : 150,
'n_epochs' : 5,
'gradient_library': "autograd",
'hyper_search' : None,
'verbose' : True,
},
batch_size_safety=1000
)
Notice in optimization_hyperparams that we are specifying 'use_batches' : True, indicating that we want to use batches in gradient descent. The batch size we request is 150, and we want to run for 5 epochs. Using batches of around this size will make gradient descent run significantly faster. If we don't use batches, we will be running every image in the candidate dataset (35,000 in this example) through the forward and backward pass of the model on every single step of gradient descent, which will be extremely slow. We should note that we had to play around with batch size, number of epochs, and the theta learning rate, alpha_theta, to get gradient descent to converge appropriately. We did not perform a proper hyperparameter optimization process, which we recommend doing for a real problem.
We also batch the safety data using batch_size_safety=1000. This passes 1000 images in the safety dataset through the model at a time during the safety test. If we exclude this parameter, all 35,000 samples in the safety dataset will be passed through the model at once. This can be extremely slow and can result in exhausting the memory of your machine. As a result, for problems with large datasets and/or large models we highly recommend using this parameter. The value of this parameter does not change the result of the safety test. The value you choose for your use case will depend on your dataset, model, and resources you have available.
Finally, we are ready to run the Seldonian algorithm using this spec object.
SA = SeldonianAlgorithm(spec)
passed_safety,solution = SA.run(debug=False,write_cs_logfile=True)
if passed_safety:
print("Passed safety test.")
else:
print("Failed safety test")
print("Primary objective evaluated on safety test:")
print(st_primary_objective)
Here is the whole script all together:
#pytorch_mnist.py
import autograd.numpy as np # Thinly-wrapped version of Numpy
from seldonian.spec import SupervisedSpec
from seldonian.dataset import SupervisedDataSet
from seldonian.models.pytorch_cnn import PytorchCNN
from seldonian.models import objectives
from seldonian.seldonian_algorithm import SeldonianAlgorithm
from seldonian.parse_tree.parse_tree import (
make_parse_trees_from_constraints)
import torch
from torchvision import datasets
from torchvision.transforms import ToTensor
if __name__ == "__main__":
torch.manual_seed(0)
regime='supervised_learning'
sub_regime='multiclass_classification'
data_folder = './data'
train_data = datasets.MNIST(
root = data_folder,
train = True,
transform = ToTensor(),
download = True,
)
test_data = datasets.MNIST(
root = data_folder,
train = False,
transform = ToTensor(),
download = True,
)
# Combine train and test data into a single tensor of 70,000 examples
all_data = torch.vstack((train_data.data,test_data.data))
all_targets = torch.hstack((train_data.targets,test_data.targets))
N=len(all_targets)
assert N == 70000
frac_data_in_safety = 0.5
features = np.array(all_data.reshape(N,1,28,28),dtype='float32')/255.0
labels = np.array(all_targets) # these are 1D so don't need to reshape them
meta_information = {}
meta_information['feature_col_names'] = ['img']
meta_information['label_col_names'] = ['label']
meta_information['sensitive_col_names'] = []
meta_information['sub_regime'] = sub_regime
dataset = SupervisedDataSet(
features=features,
labels=labels,
sensitive_attrs=[],
num_datapoints=N,
meta_information=meta_information)
constraint_strs = ['ACC >= 0.95']
deltas = [0.05]
parse_trees = make_parse_trees_from_constraints(
constraint_strs,deltas,regime=regime,
sub_regime=sub_regime)
device = torch.device("mps")
model = PytorchCNN(device)
initial_solution_fn = model.get_initial_weights
spec = SupervisedSpec(
dataset=dataset,
model=model,
parse_trees=parse_trees,
frac_data_in_safety=frac_data_in_safety,
primary_objective=objectives.multiclass_logistic_loss,
use_builtin_primary_gradient_fn=False,
sub_regime=sub_regime,
initial_solution_fn=initial_solution_fn,
optimization_technique='gradient_descent',
optimizer='adam',
optimization_hyperparams={
'lambda_init' : np.array([0.5]),
'alpha_theta' : 0.001,
'alpha_lamb' : 0.01,
'beta_velocity' : 0.9,
'beta_rmsprop' : 0.95,
'use_batches' : True,
'batch_size' : 150,
'n_epochs' : 5,
'gradient_library': "autograd",
'hyper_search' : None,
'verbose' : True,
},
batch_size_safety=1000
)
SA = SeldonianAlgorithm(spec)
passed_safety,solution = SA.run(debug=False,write_cs_logfile=True)
if passed_safety:
print("Passed safety test.")
else:
print("Failed safety test")
print("Primary objective evaluated on safety test:")
print(st_primary_objective)
If you save this script to a file named pytorch_mnist.py and run it like:
$ python pytorch_mnist.py
You will see the following output:
Have 5 epochs and 234 batches of size 150 for a total of 1170 iterations
Epoch: 0, batch iteration 0
Epoch: 0, batch iteration 10
Epoch: 0, batch iteration 20
Epoch: 0, batch iteration 30
Epoch: 0, batch iteration 40
...
Epoch: 4, batch iteration 200
Epoch: 4, batch iteration 210
Epoch: 4, batch iteration 220
Epoch: 4, batch iteration 230
Wrote /Users/ahoag/beri/code/engine-repo-dev/examples/pytorch_mnist_batch/logs/candidate_selection_log10.p with candidate selection log info
Have 35 batches of size 1000 in safety test
Passed safety test.
Primary objective evaluated on safety test:
0.0812836065524022
The whole script takes about 90 seconds to run on my M1 Macbook Air using the 8-core GPU, and about 5 minutes to run on the CPU. The location of the candidate selection log info file will be in a logs/ subfolder of wherever you ran the script. The safety test should also pass for you, though the value of the primary objective (cross entropy over all 10 classes) on the safety test might differ slightly because your machine's random number generator may differ from mine. The important thing is that the gradient descent curve is similar. Plot it using the following Python code, replacing the path to the logfile with the location where that file was saved on your machine.
from seldonian.utils.plot_utils import plot_gradient_descent
from seldonian.utils.io_utils import load_pickle
logfile = "/Users/ahoag/beri/code/engine-repo-dev/examples/pytorch_mnist_batch/logs/candidate_selection_log10.p"
sol_dict = load_pickle(logfile)
plot_gradient_descent(sol_dict,'cross entropy')
You should see a similar plot to this one:
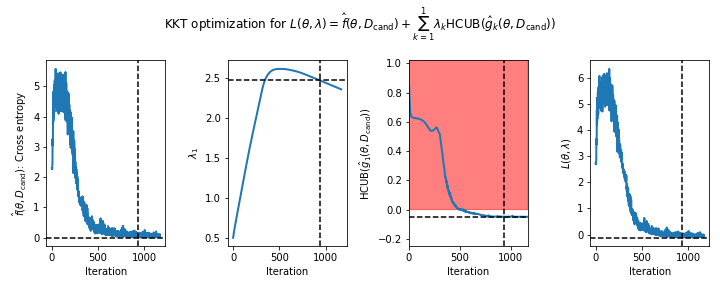Figure 1 - How the parameters of the Lagrangian optimization problem changed during gradient descent on the MNIST task. The panels show the values of the (left) primary objective $\hat{f}(\theta,D_\mathrm{cand})$ (in this case the cross entropy), (middle left) single Lagrange multiplier, ${\lambda_1}$, (middle right) predicted high-confidence upper bound (HCUB) on the constraint function, $\hat{g}_1(\theta,D_\mathrm{cand}) = \text{ACC} - 0.95$, and (right) the Lagrangian $\mathcal{L}(\theta,\lambda)$. The dotted lines indicate where the optimum was found. The optimum is defined as the feasible solution with the lowest value of the primary objective. A feasible solution is one where $\mathrm{HCUB}(\hat{g}_i(\theta,D_\mathrm{cand})) \leq 0, i \in \{1 ... n\}$. In this example, we only have one constraint. The infeasible region is shown in red in the middle right plot. The feasible region is shown in white in the same plot. The noise in the curves for $\hat{f}$ and $\mathcal{L}$ is due to the fact that we batched the candidate data in gradient descent.